[最も選択された] 縁の面積 350113-縁の面積 公式
半径4cm・高さ6cmの円柱 ※円周率を314とした場合 円の面積=4cm×4cm×314=5024cm 2 円の円周=4cm×2×314=2512cm 側面の面積=6cm×2512cm=cm 2 円柱の面積=5024cm 2 5024cm 2 cm 2 =2512cm 2 ※円周率をπとした場合6年算数 円の面積1 子どもの学習支援 by いっちに算数 スマホ版 「円周率と円周と直径・半径」の勉強を忘れている時は、5年の「円と正多角形」でおさらいをしまょう。 「長方形・正方形の面積」の求め方を忘れている時は、4年の「面積」でおさらいをしましょう。円の面積を求める公式は小学校で習いますが、なぜその公式になるのか?という 疑問 (ぎもん) は、高校2年生で 微分 (びぶん) を学習するまで分かりません!下のリンクでは、図形的に公式を 理解 (りかい) してもらう方法を 紹介 (しょうかい) しています。

円の4分の1の面積の求め方を教えてください Clearnote
縁の面積 公式
縁の面積 公式- 円の面積の公式はご存じの通り、πr 2 である。 πは円周率、rは半径だ。 ではなぜ、この式になるのだろうか。 様々な証明方法があるが、まず円の面積はどのように求めればよいでしょうか? ここでも既に答えが分かっているかもしれませんが、同様に なぜ、そうなるのか? というのを一緒に考えてみてください。 ヒントは同じく「平行四辺



円の面積と公式 面積計算機
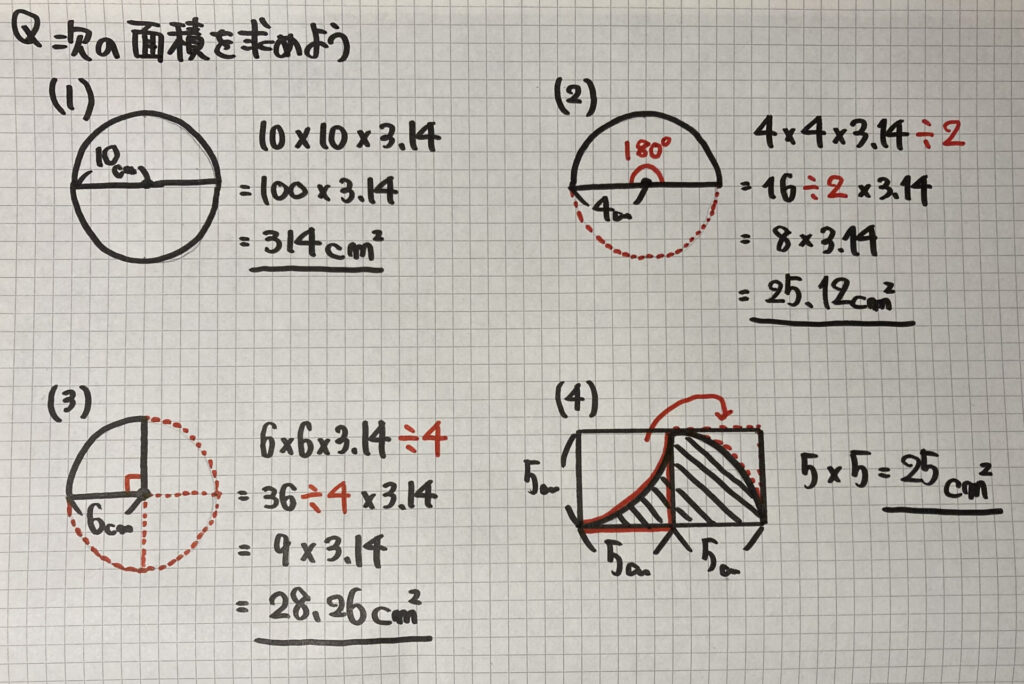
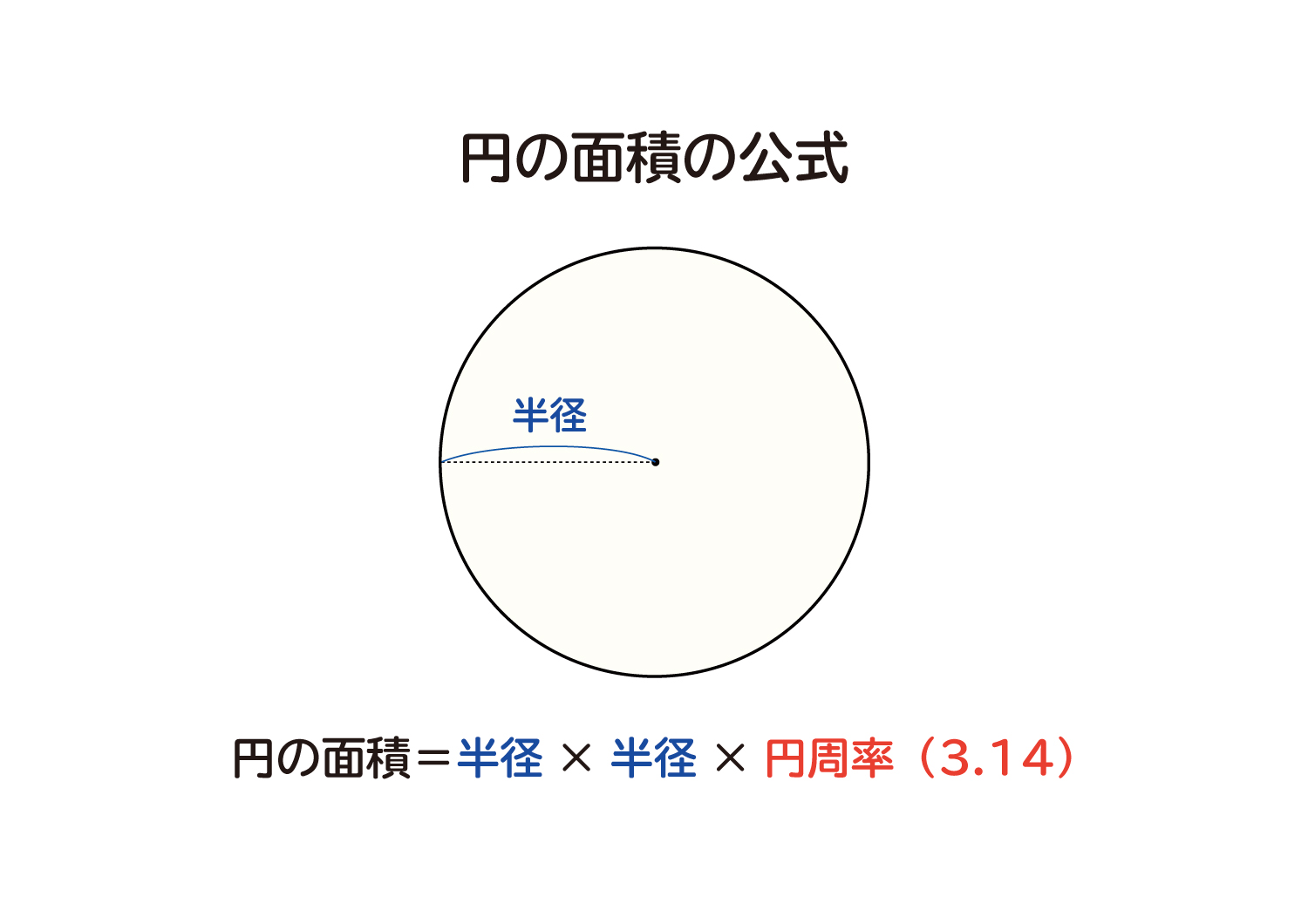
円の面積 円の面積は,半径×半径×314で求められます。 この求積公式の指導にあたっては,公式の理解はもとより,そこに至る過程を大切に指導することが重要です。 まず,半径10cmの円の面積が半径 (10cm)を1辺とする正方形の面積のおよそ何倍になるか ここではこんなことを紹介しています↓ 円の面積の公式はなぜ「\\(π\\)×\\(r\\)×\\(r\\)」と表現できるのでしょうか? ここではそんな疑問に対して、図形を使った簡単な公式のイメージ方法を紹介します。 先に言っておくと、ここで紹介する方法は円の面積の厳密な証明方法ではありません 円の面積 円の面積と円周の公式はどっちがどっちだか わからなくなることがありますのでしっかり確実に覚えておくようにしましょう。 円の面積 = 半径 × 半径 × 円周率 弧の面積 まず、円の面積を求めて、そのうちの弧の角度分の面積を知りたいの
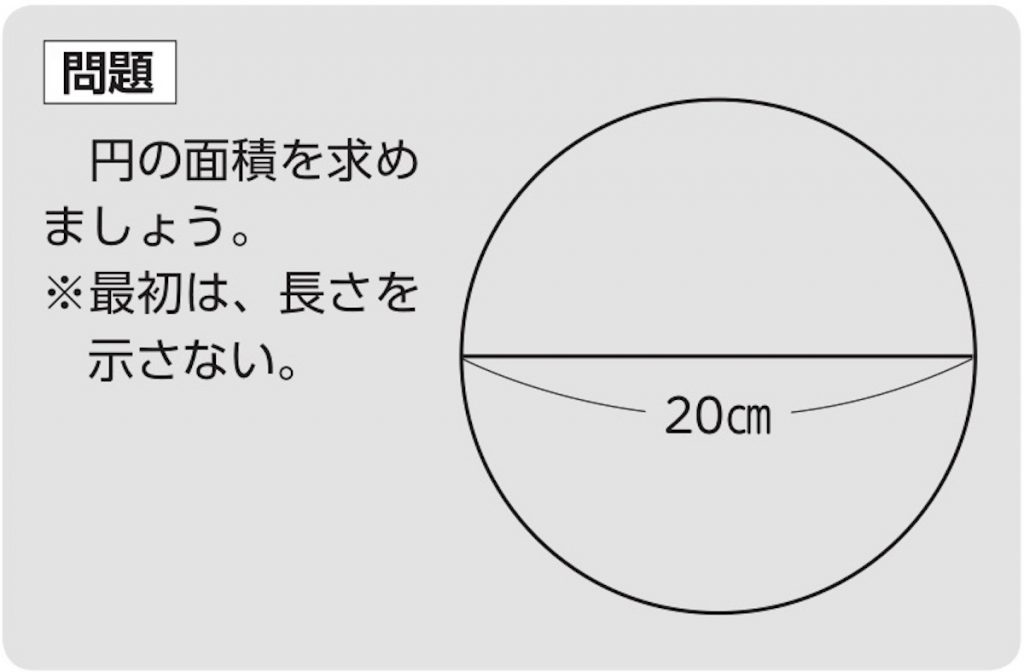
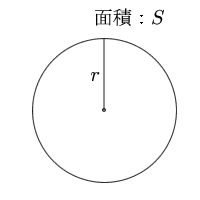
今回は小学校の算数で勉強する、円の面積・円周の求め方について書いていきたいと思います。(年6月日追記しました。) 円周の求め方公式 円の面積の求め方公式 円の面積・円周の長さを求める問題 問題① 《円の面積の求め方》 《円周の長さの求め方》 問題② 《円周 例えば、円の面積が関わる問題では 円の半径を $2$ とするとき、この円の面積を求めよ。 円の面積を $4\pi$ とするとき、この円の直径を求めよ。 円の面積を $4\pi$ とするとき、この円の円周の長さを求めよ。 このように、たくさんの問題パターンが考え円の面積の解説 円の面積は 半径×半径×円周率=面積 で求めることができます。 半径をr、円周率をπ、面積をSとすると S=πr2 となります。 円の面積を求める公式 面積=半径×半径×円周率 半径3cmの円の面積は何cm 2 ? ※円周率を314とした場合 → 3cm×3cm×
円の面積は直径を用いると面積=直径^2/4 × 円周率π によって求めることができます。 なお、半径を用いると、円の面積=半径×半径×314となります。 エクセルで円の面積を求めるには、この公式を数式中に組み込んでいけばいいわけです。円の面積の公式の導出 アルキメデスによる証明から、命題1における円周の長さを 、半径を とすると、円の面積 は底辺が 、高さが の直角三角形の面積なので、円の面積の初等的な求め方は簡単だ。 でも、そこには積分の初期的な概念がある。 では、その初歩的な概念から積分へはどうやって至るのだろうか。 その積分を身体で感じるために、簡単に求まる円の面積を積分で求めてみよう。



小6算数 円の面積とおうぎ形 の問題 どこよりも簡単な解き方 求め方 かずのかずブログ




6年 円の面積まとめプリント ネコ好きな学校の先生の日常
円の面積を計算するには、 pi関数 指数と一緒に オペレーター (^)。示されている例では、コピーされたc5の式は次のとおりです。 = pi * b5 ^ 2 これは、列bで指定された半径を持つ円の面積を計算し 円の面積 = 一辺の長さを円の半径とした正方形の面積 * 円周率 円周率の求め方 ここで、上の式を円周率について解くように整理してみましょう! 下記のように書き換えることができるはずです。 円周率 = 円の面積 / 一辺の長さを円の半径とした正方形の面積 円の面積は、 「半径 × 半径 × 314」 (半径 × 半径 × 円周率 \(π\) )という公式で求めることができます。 例題①半径 \(2\) cmの円の面積を求めて下さい。 答え: \(2 × 2 × 314=1256\)(cm 2) 正確には \(2 × 2 × π=4π\)




円の面積 Youtube



なぜ 円の面積は 半径 半径 円周率 3 14 なのか を説明します おかわりドリル
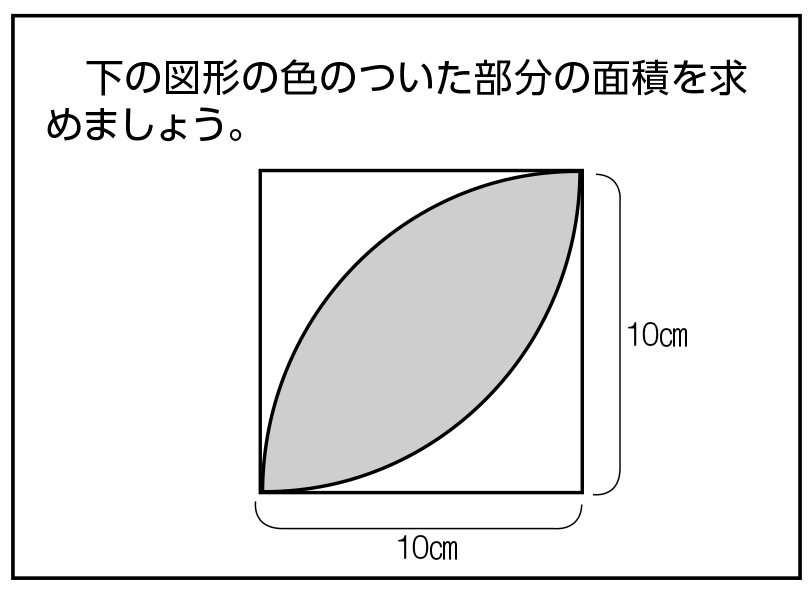
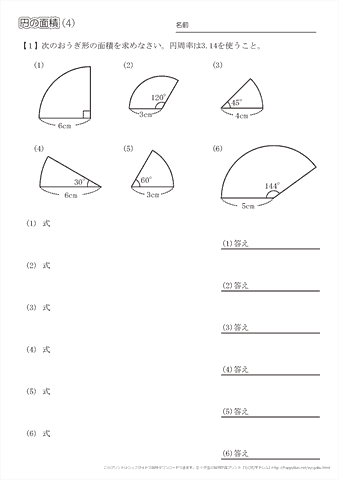
大きい円の面積と、大きい円の中にある半円の面積4つ分の差は、 =㎠ よって、 答え ㎠ 面積④ 重なりや移動でできた面積 例題5 長方形と正方形が下の図のように重なっています。色の付いた部分の面積を求めなさい。発展問題 1 2 3 4 5 6 7 円の面積を速く正確に計算するために、円周率×1けたの数の答えをおぼえましょう。6年「円の面積」 氏名 1 次の円の面積は何㎠ですか。 ⑴ 半径4cmの円 半径 × 半径 × 314 = 円の面積 式 答え ⑵ 半径8cmの円 式 答え ⑶ 直径14cmの円 直径 ÷ 2 = 半径 式 半径 × 半径 × 314 = 円の面積 答え ⑷ 直径18cmの円 式 答え



世界一やさしい 円の面積を求める問題の解き方 働きアリ



面積 円の面積の変わった求め方の問題 数学の要点まとめ 練習問題一覧
円 面積計算 公式 求め方 計算方法 直径 半径 自動 円周率 計算機 履歴機能付きAbout Press Copyright Contact us Creators Advertise Developers Terms Privacy Policy & Safety How works Test new features Press Copyright Contact us Creators 円の面積、球の体積の公式の微積による証明(導出) そもそもこれは微積を用いないと厳密には証明できない感じです。 球の体積公式まずは公式を書いておきます。半径を \(r\) として\(V=\displaystyle\frac{4}{3}\p



円の面積 円周の求め方 公式 小学生 中学生の勉強



小6算数 円の面積 指導アイデア 2 みんなの教育技術
スポンサーリンク 円の面積 \(=\) 半径 \(\times\) 半径 \(\times\) 円周率 それでは「円の面積の公式」を使った「練習問題」を解いてみましょう。 練習問題① 半径が 2(cm)の円の面積を求めて 円の面積と円周の長さ 円の面積 (S) = 円周の長さ (L) × 半径 (r) ÷ 2 円の面積 (S) = 円周の長さ (L) 2 ÷ 円周率 (π) ÷ 4 著者 やまでら くみこ スポンサーリンク円の面積の公式 円の面積は 『半径×半径×円周率』 で計算できます。 たとえば以下のような問題の場合。 例題 半径 2cm 2 c m の円の面積を求めよ。 答えはこのように求めることができます。 2 ×2× 314=1256(cm2) 2 × 2 × 314 = 1256 ( c m 2) つづいて、なぜ



3匹の子ブタと円の面積




6年算数 円の面積 なぜ 半径 半径 円周率になるのか 解説します Youtube
解説 答え:∠BAC=55° 半円の問題(気が付きにくい円周角と中心角2) 線分CDを直径とする半円があり、点Oは線分CDの中点である。 また、半円上に点A、Bがある。 (1)∠OBC=65°のとき、∠DABの大きさを求めよ。 解説 答え:∠DAB=115° (2)∠DAB=1°、線分CD=10=d 2 =(転動円の面積)×3 =8r=4d A=面積 C=円周 A=πr 2 =r 2 =d 2 c=2πr=622r=d 中心角1°に対する弧の長さ=d 中心角n°に対する弧の長 円の面積 半径 半径 円周率 円 の 面 積 = 半 径 × 半 径 × 円 周 率 = 4 × 4 × 314 = 5024 c m 2 と求まります。 問②面積が c m 2 の円の円周の長さを求めてください。 (円周率は 314 ) 円の面積の公式から半径を計算したあと 「半径⇒直径⇒円周の
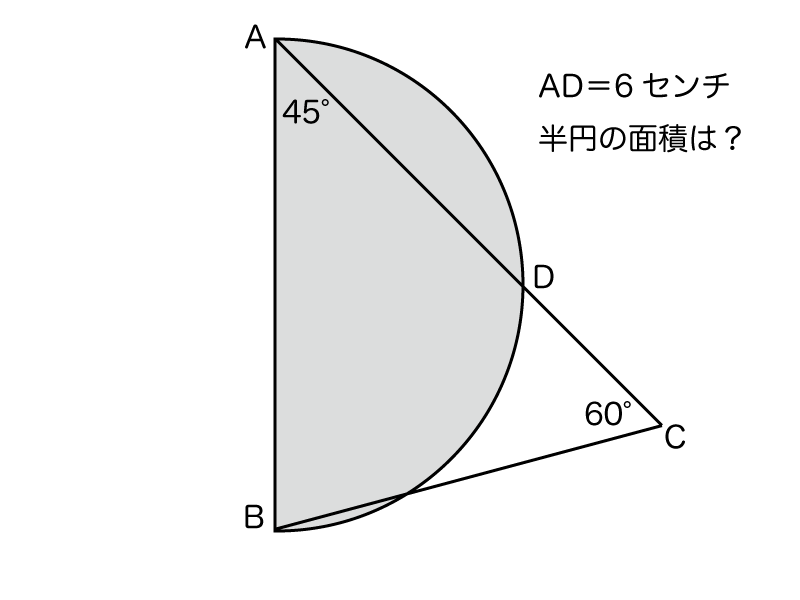



面積公式を組み合わせて解く半円の面積計算 受験算数入門



小学6年生の算数 円の面積 問題プリント ちびむすドリル 小学生
円の面積を求める日が来るとは。 助かりました、ありがとうございます。 4 1703 50歳代 / エンジニア / 非常に役に立った /円の面積 「半径×半径×円周率」で求められる円の面積。 いろいろな大きさの円の面積を計算してみよう。 動画で学ぼう! (NHK for School) 円の面積の求め方を、四角に直すことで原理から考える円の面積を求める公式は、S = πr^2 で表されます。このページでは、円の面積の求め方を、計算問題と共に説明しています。また、公式の導き方のイメージも説明しています。




円の面積3 小学校6年生の教科書から つづき 身勝手な主張



円の面積の公式 算数の公式
小学6年生で習う、円の面積の問題の解き方を世界一やさしく解説します。 ★今から学ぶこと 1、円の面積を求める式円の面積=半径×半径×314 2、円の一部の面積を求める式円の面積の一部=半径×半径×314×中心の角/360° 3、色(かげ)がついた部分の面積の求め方全体白い部分 ★こ円の直径D=8cmです。よって円の面積Aは、 です(π=314で計算)。 円の直径から面積に変換する公式は、数学だけでなく物理や工学でも使います。必ず覚えておきましょう。直径、円の面積の詳細は下記が参考になります。 φと直径の関係は?円の面積 ツイート 面積の計算 ・ 正三角形の面積 ・ 三角形の面積 (底辺と高さ) ・ 三角形の面積 (2辺と間の角度) ・ 三角形の面積 (1辺と両端の角度) ・ 三角形の面積 (3辺の長さ)



小6算数 円の面積 指導アイデア みんなの教育技術



なぜ 円の面積は 半径 半径 円周率 3 14 なのか を説明します おかわりドリル
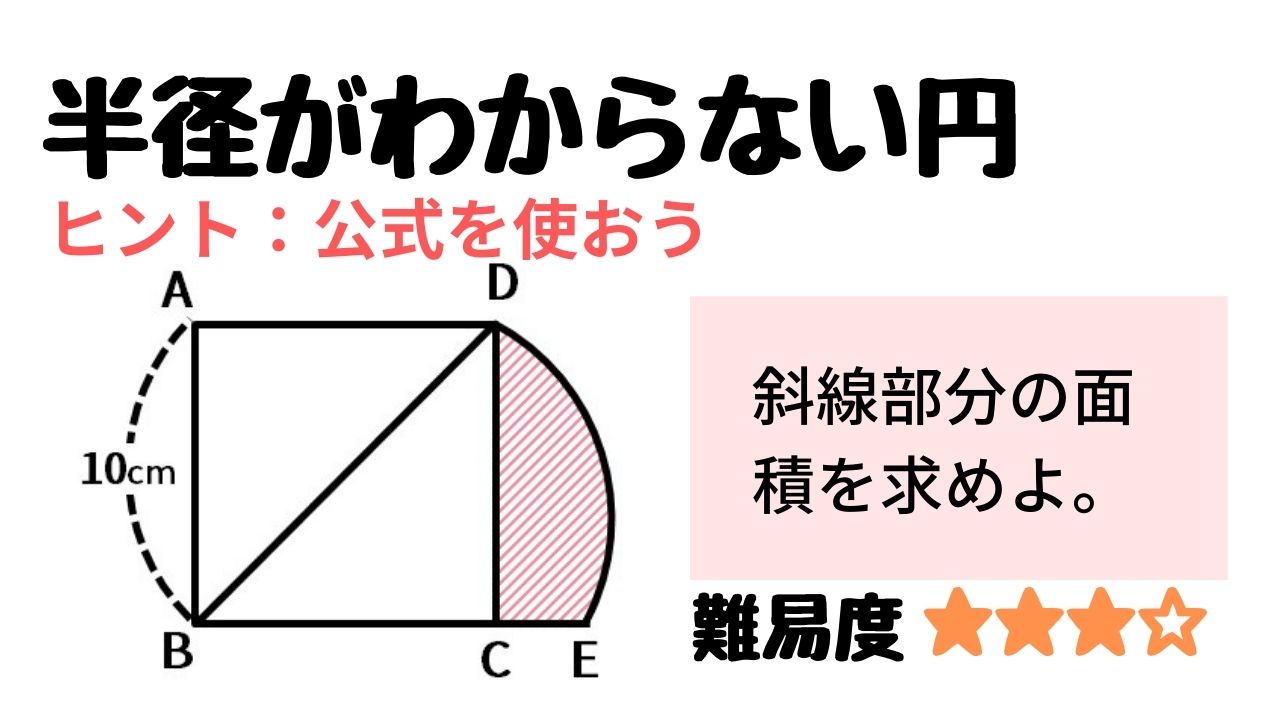



中学受験算数 半径がわからない円の面積の問題 テクニック伝授 Stupedia



円の面積 直径 半径 円周の計算機 公式を使った求め方も紹介 やまでら くみこ のレシピ
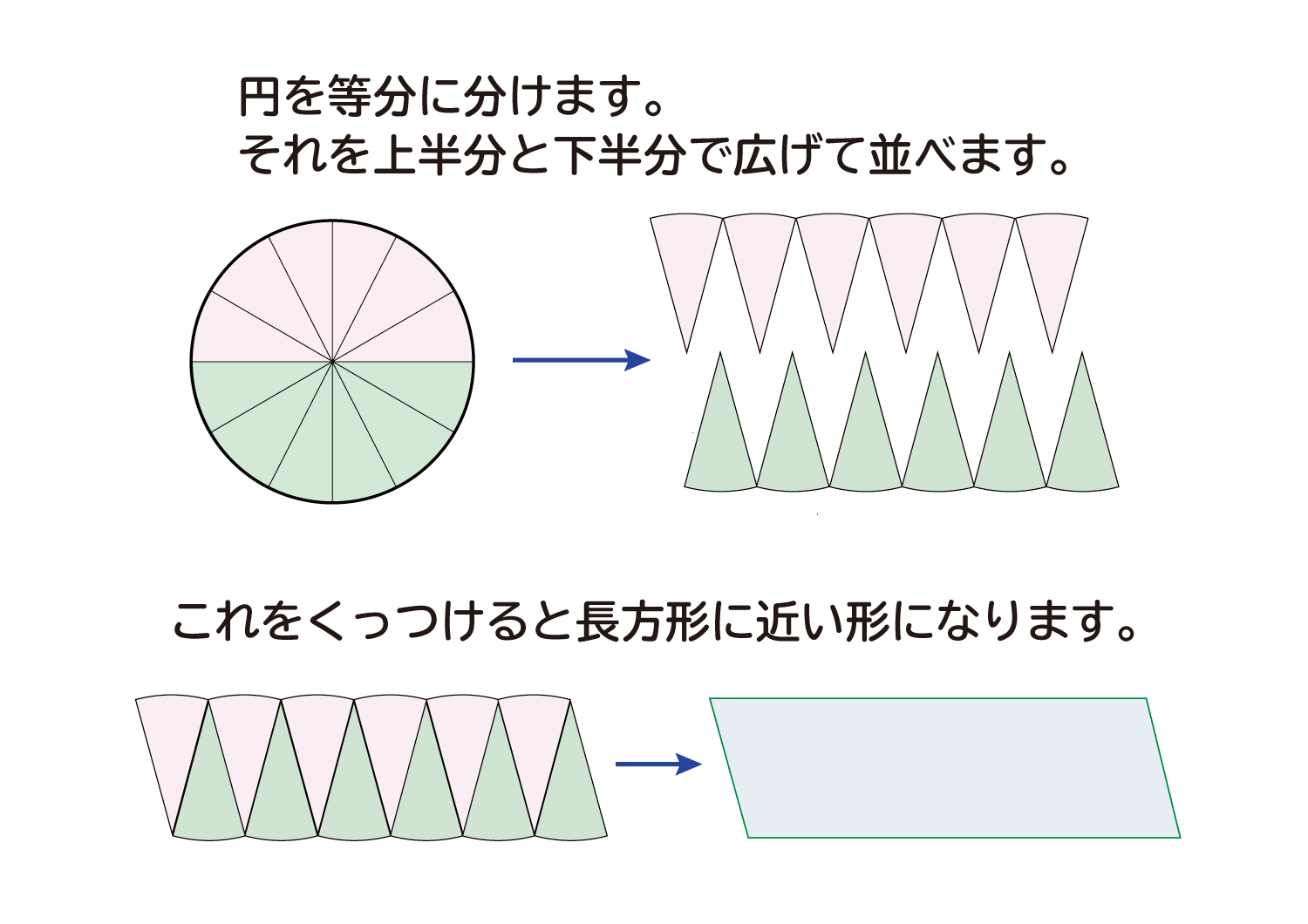



なぜ 円の面積は 半径 半径 円周率 3 14 なのか を説明します おかわりドリル




Sapix サピックス 4年 みんな知らない 円の面積 正方形 3 14 です たぶお Sapix サピックス A1 養成講座




小6 算数 小6 旧 円の面積 Youtube



円の面積 直径
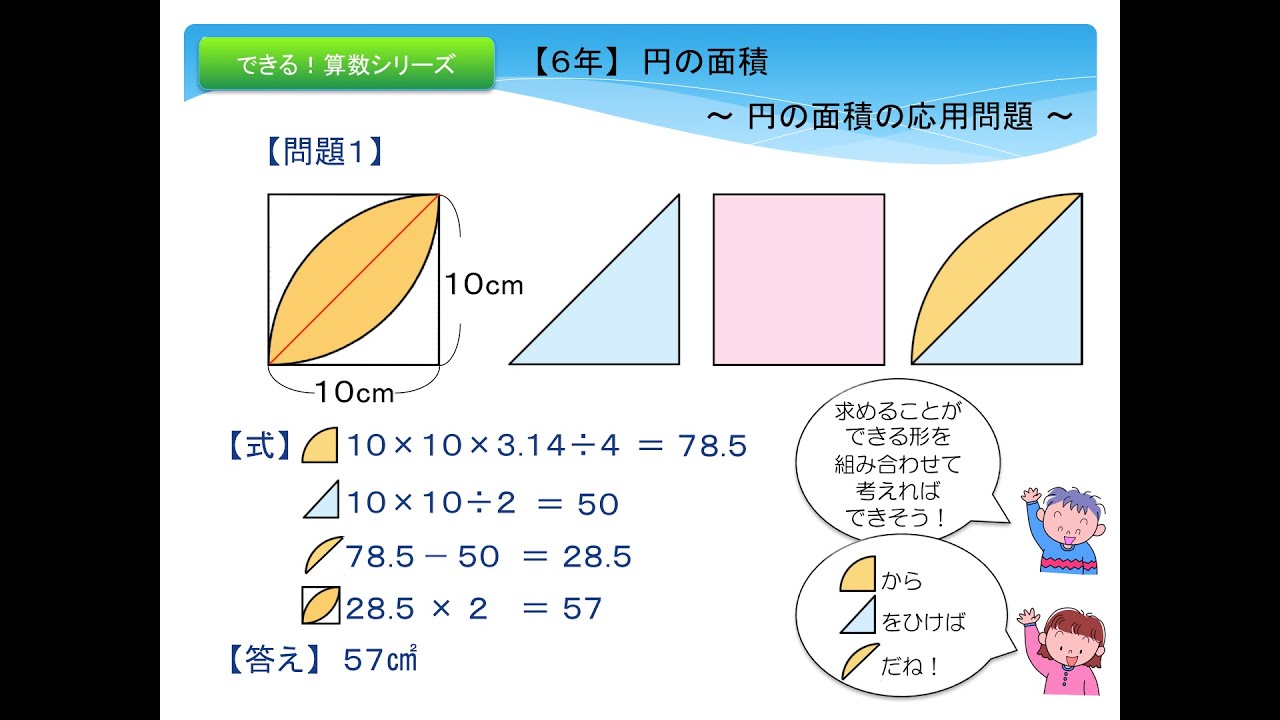



スマホok 6年 円の面積 円の面積の応用問題 Youtube
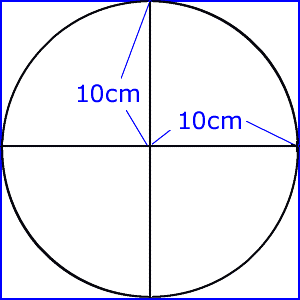



6年算数 円の面積 1 アニメでわかる教え方



算数 三日月形 半円 の面積の応用問題の答 なるほどの素
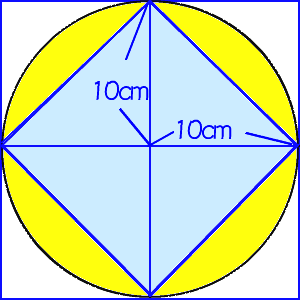



6年算数 円の面積 1 アニメでわかる教え方



円の面積
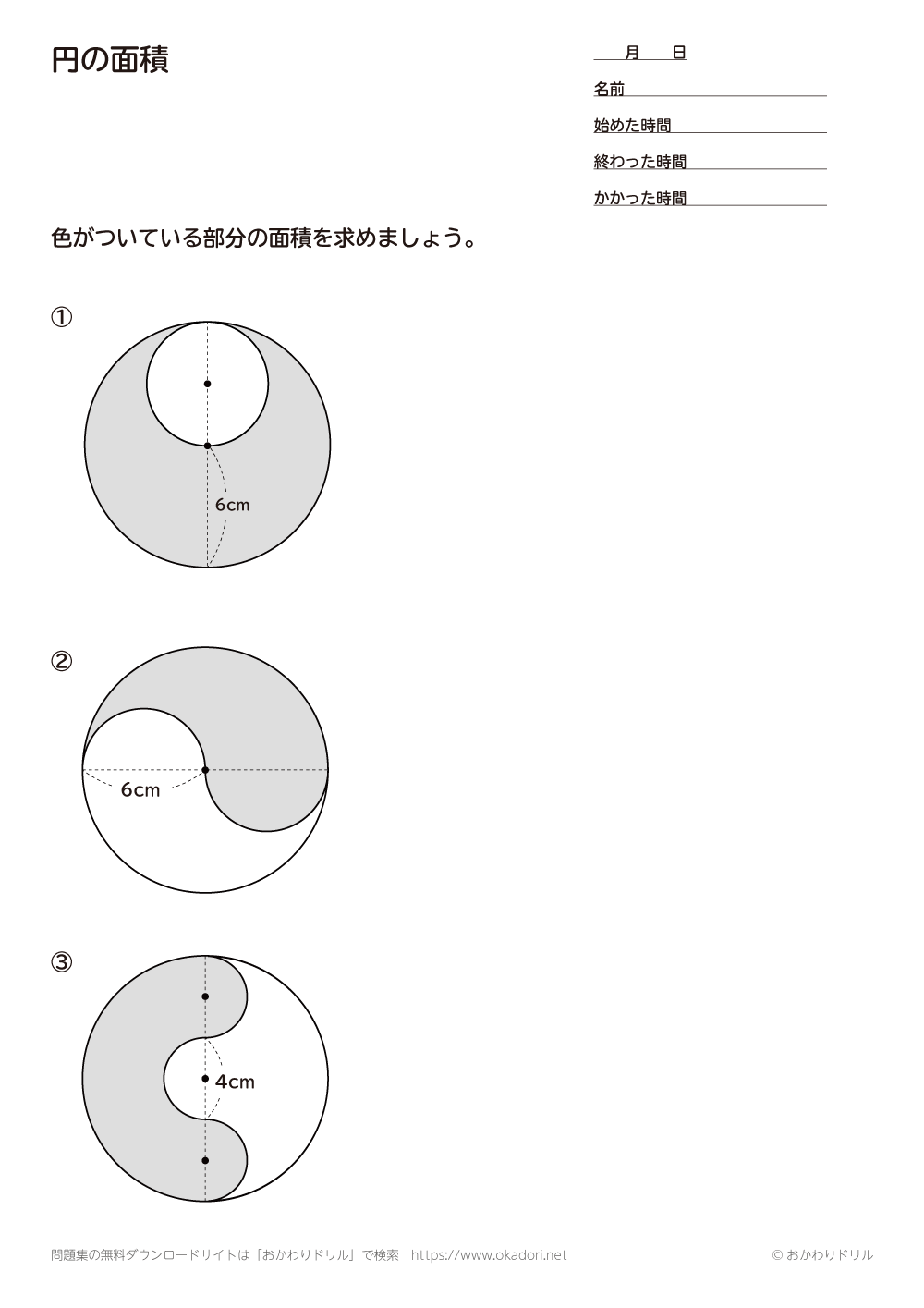



小学6年生 算数 無料問題集 円の面積 おかわりドリル




扇形の弧の長さと面積 小学 中学数学での平面図形の求め方 リョースケ大学
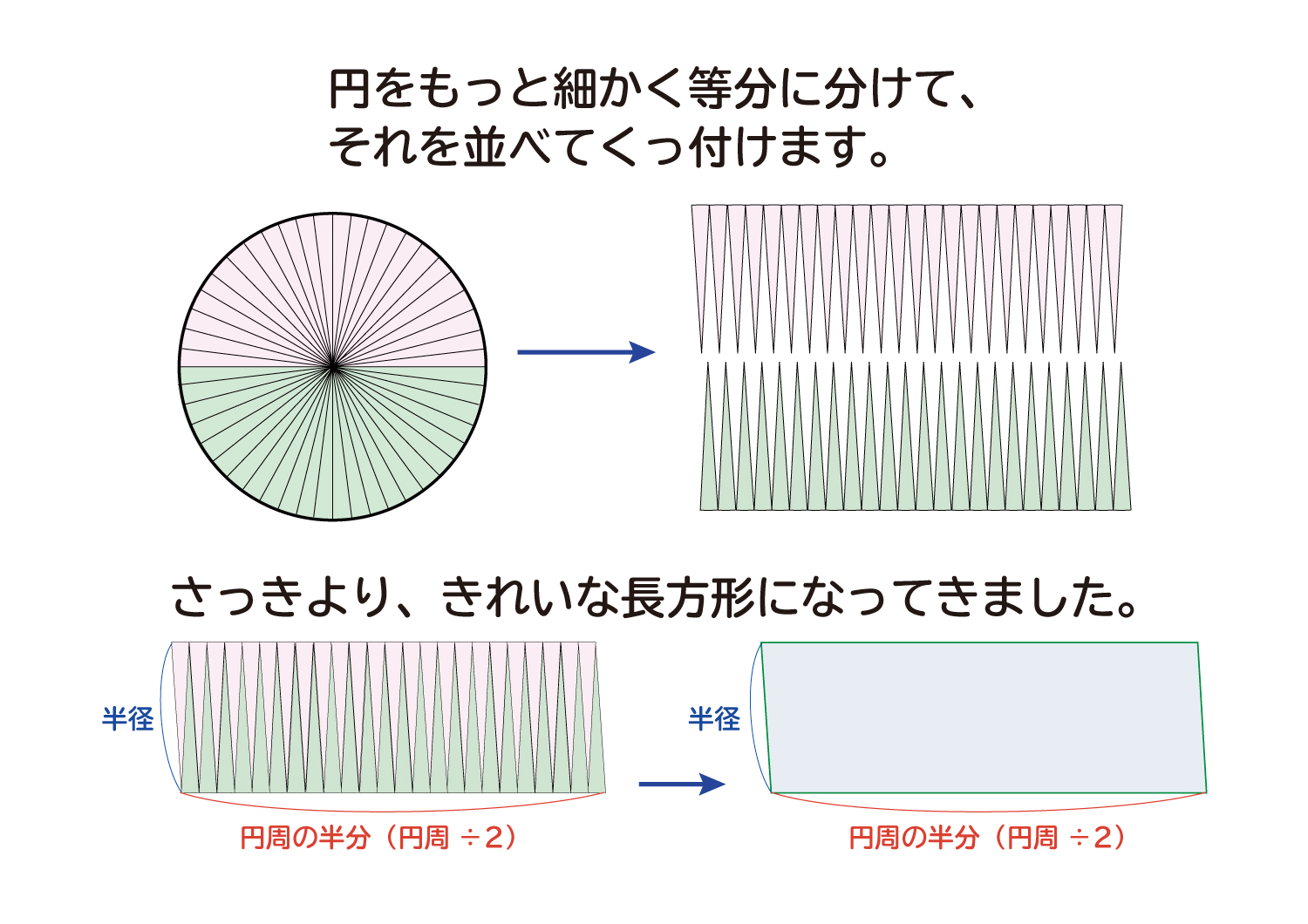



なぜ 円の面積は 半径 半径 円周率 3 14 なのか を説明します おかわりドリル




円の面積2 小学校6年生の教科書から 身勝手な主張




円の面積の応用 小学校6年算数より 身勝手な主張




円の面積



円の面積と公式 面積計算機
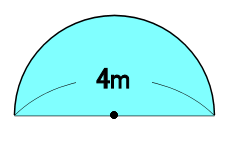



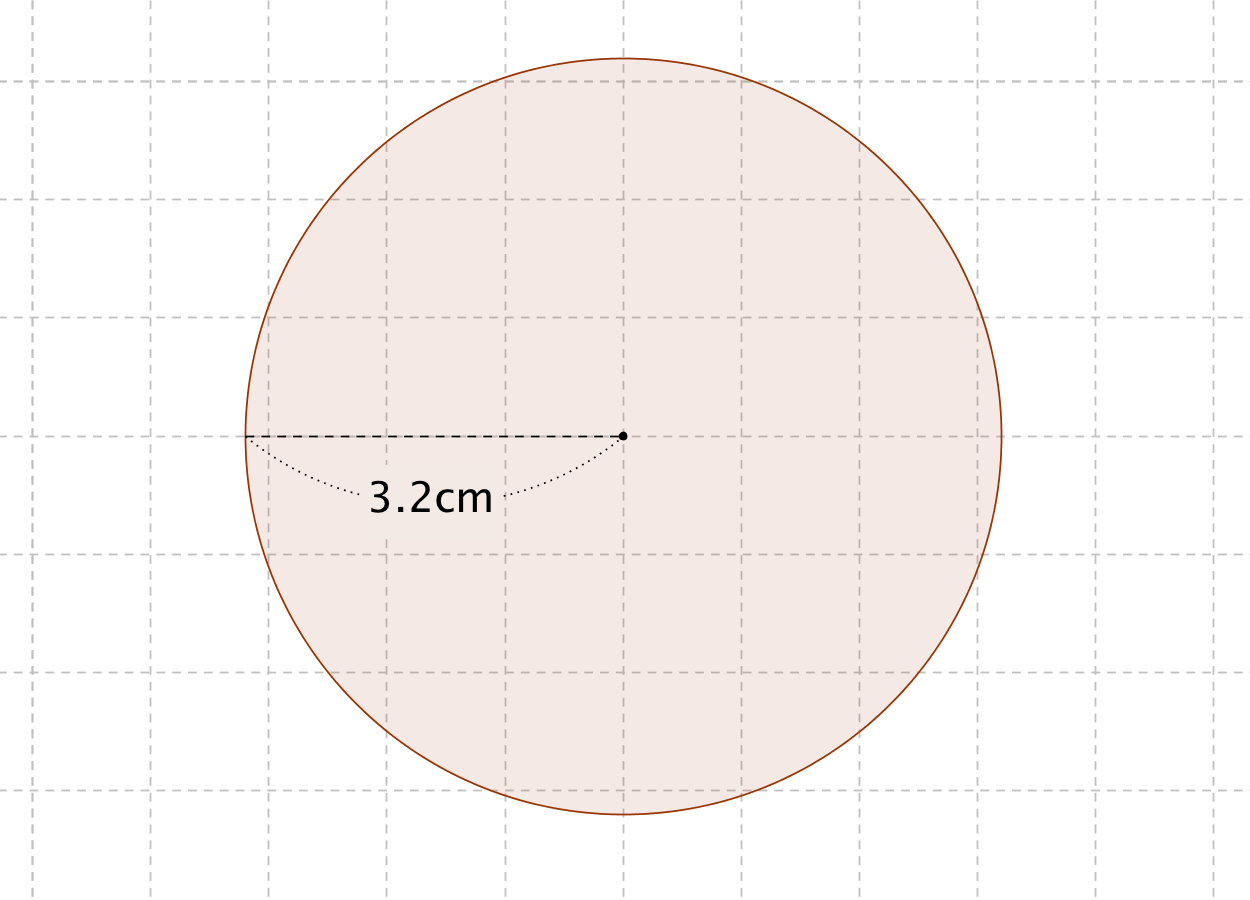
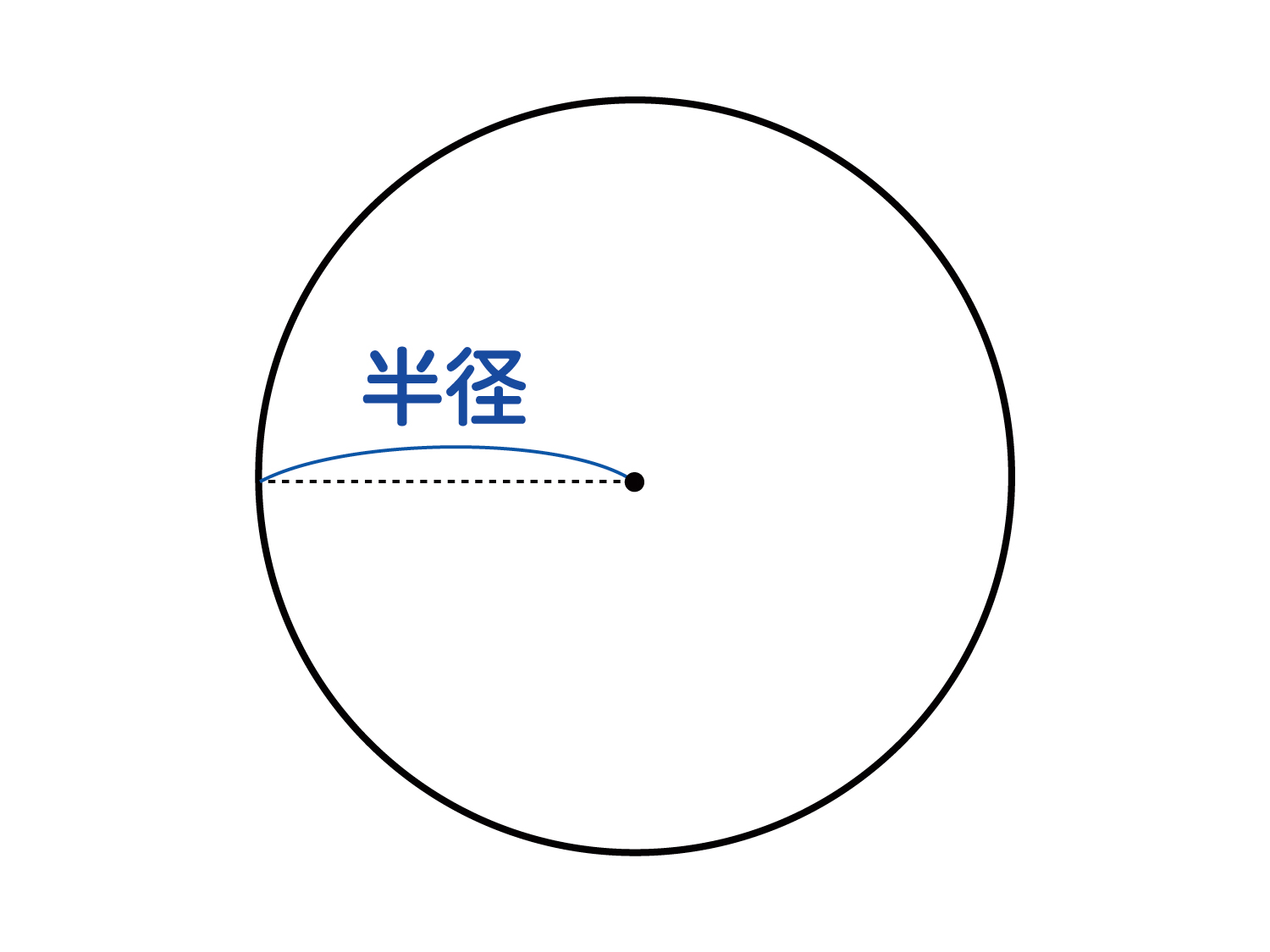
円の面積 半径



なぜ円の面積 P 半径 半径 なのでしょうか 簡単に証明方法はあるのでしょうか Quora
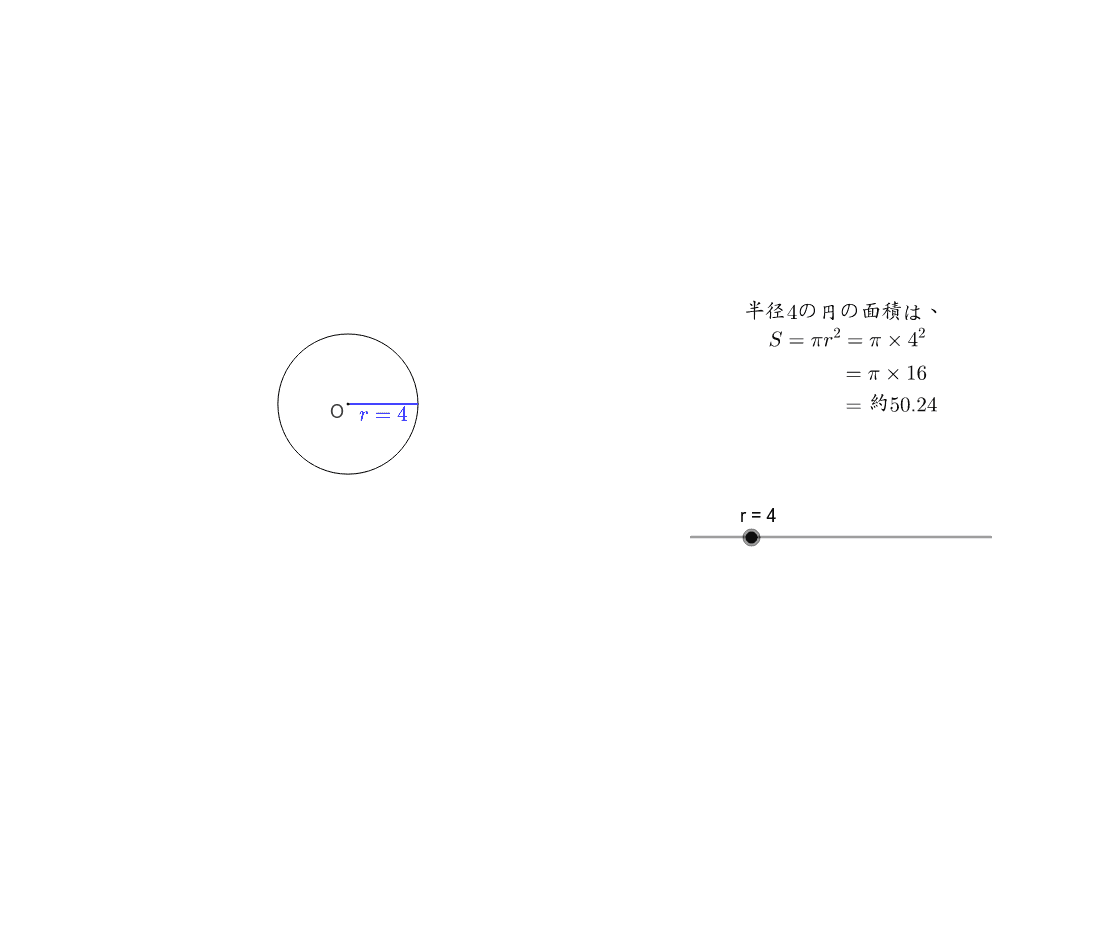



円の面積を表す文字式 Geogebra




小学6年生の算数 円の面積 問題プリント ちびむすドリル 小学生
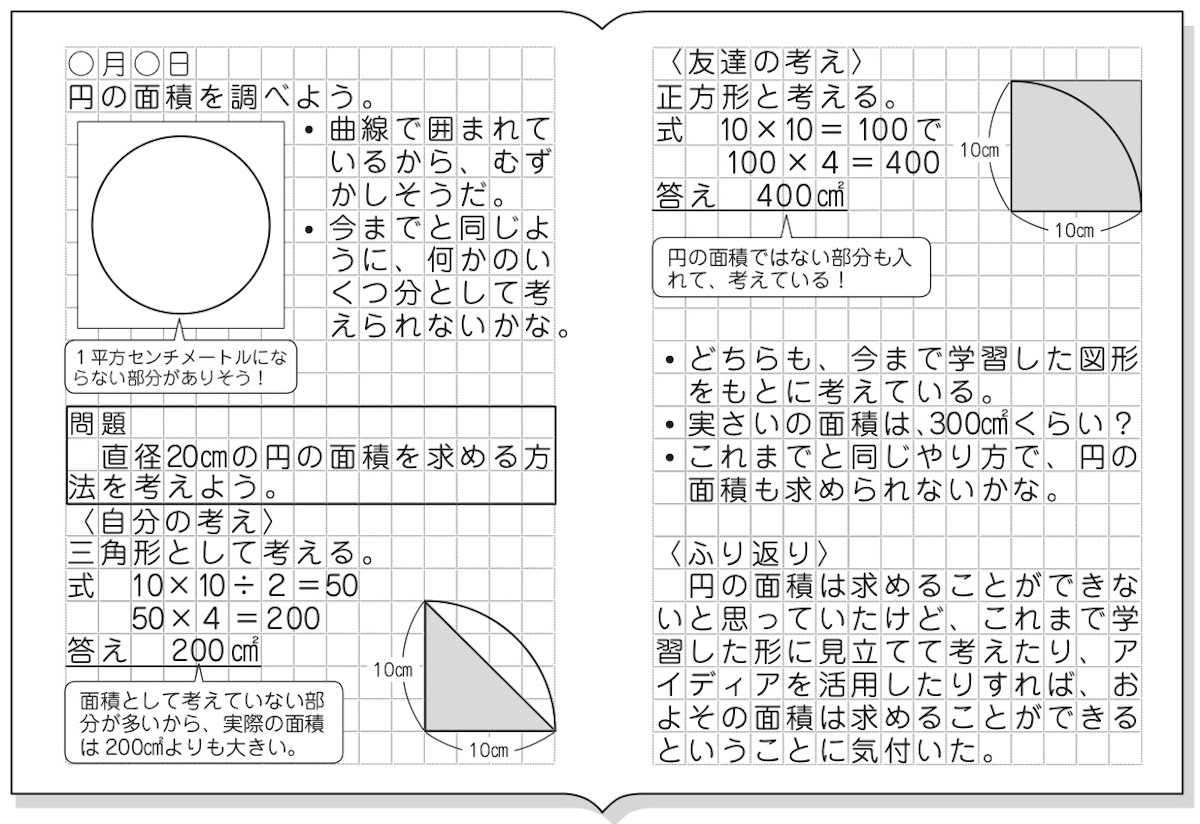



小6算数 円の面積 指導アイデア みんなの教育技術




円の4分の1の面積の求め方を教えてください Clearnote
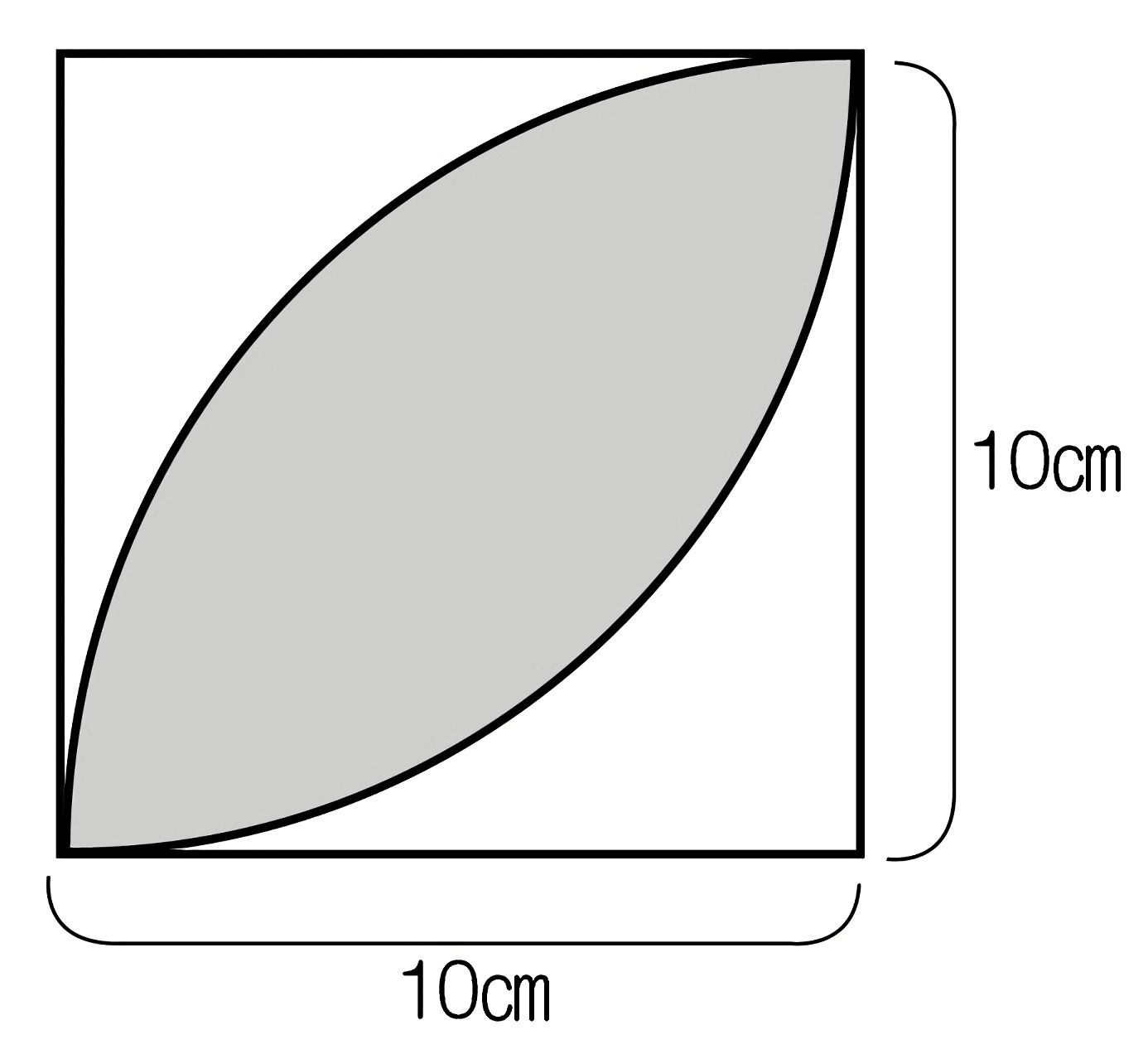



小6算数 円の面積 指導アイデア 2 みんなの教育技術




6年生算数ドリル 円




円 半円 弧 扇形 の円周 面積の求め方と公式一覧 小学生の算数 Yattoke 小 中学生の学習サイト
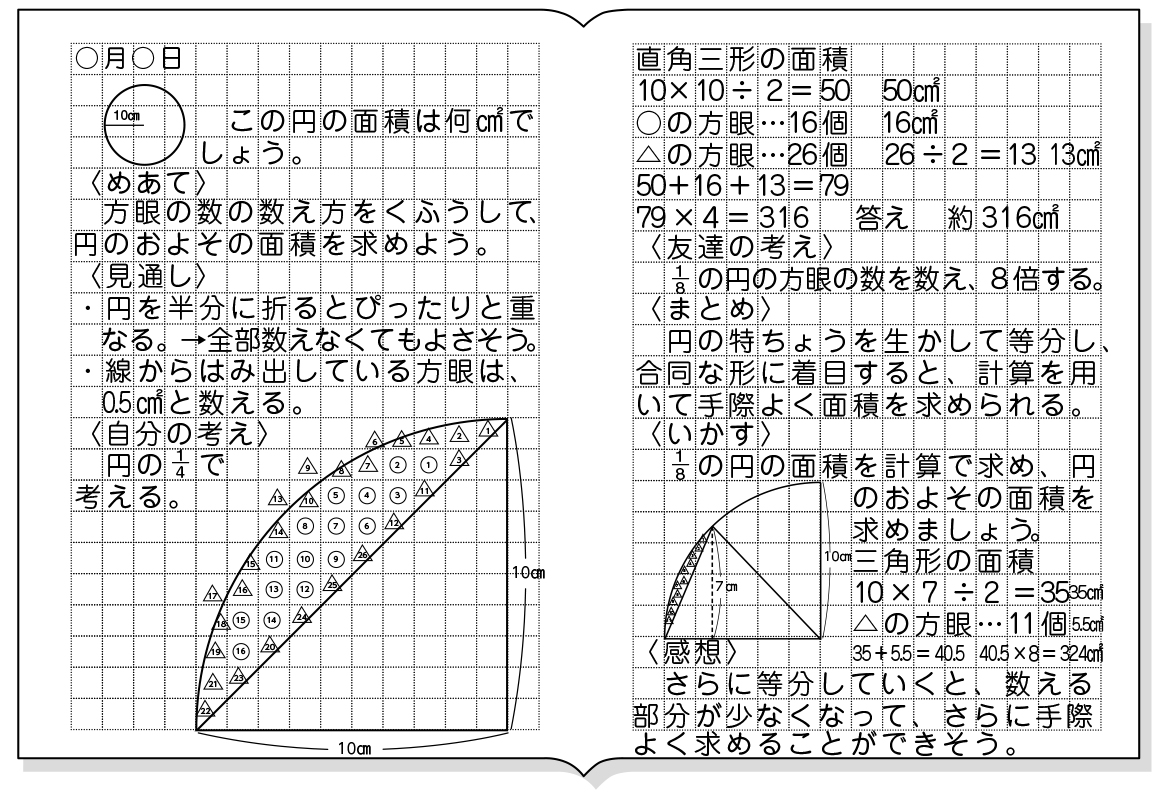



小6算数 円の面積 指導アイデア 1 みんなの教育技術
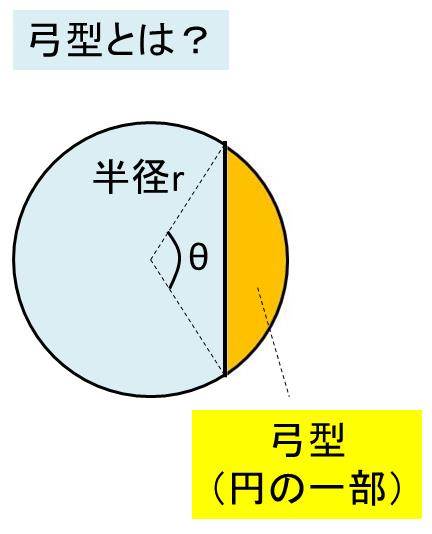



欠けた円 欠円 や弓形の面積の計算方法




円周の求め方と円の面積について アタリマエ




円の面積の公式 なぜ半径と円周率で求められるのか を小学生に分かりやすく説明する方法 数学fun
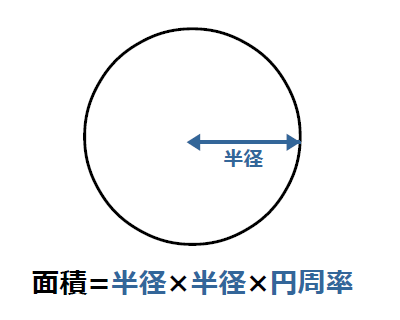



円の面積計算 ゆるゆるプログラミング
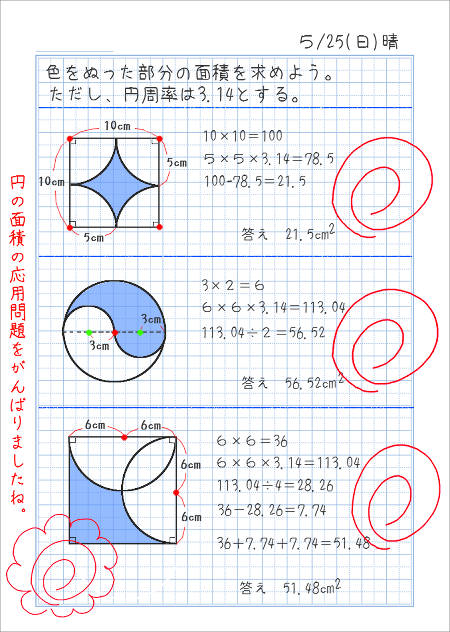



円の面積 その2 家庭学習レシピ




円 扇形 の面積 周や弧の長さの公式 数学fun



世界一やさしい 円の面積を求める問題の解き方 働きアリ The 2nd



1




円の面積の公式 算数の公式
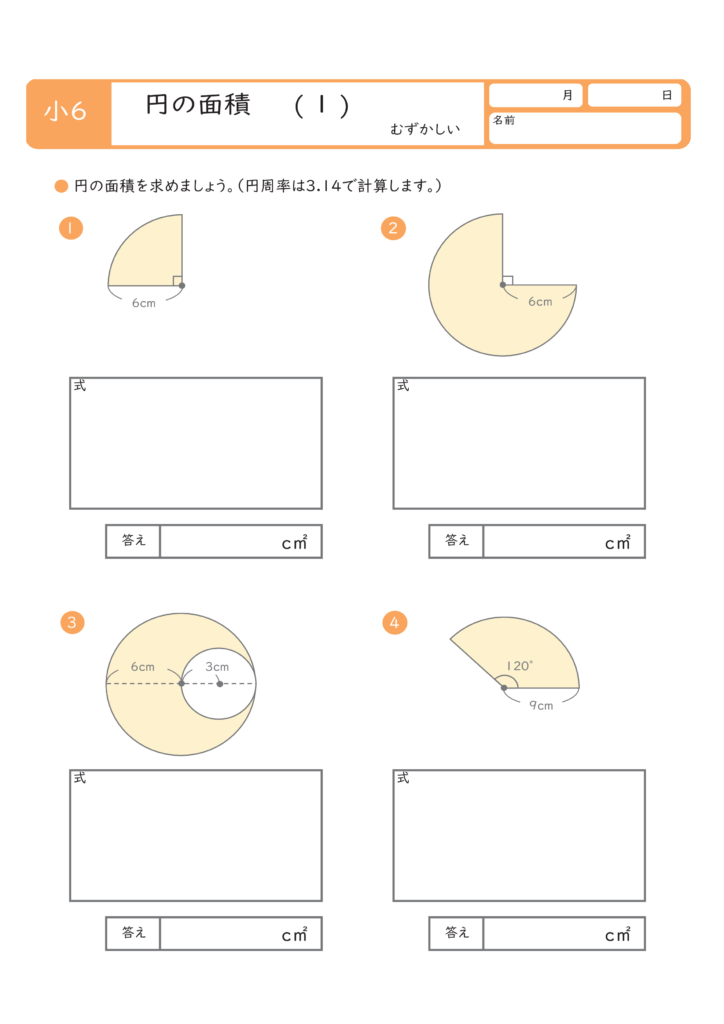



こどもプリント 円の面積 無料プリント



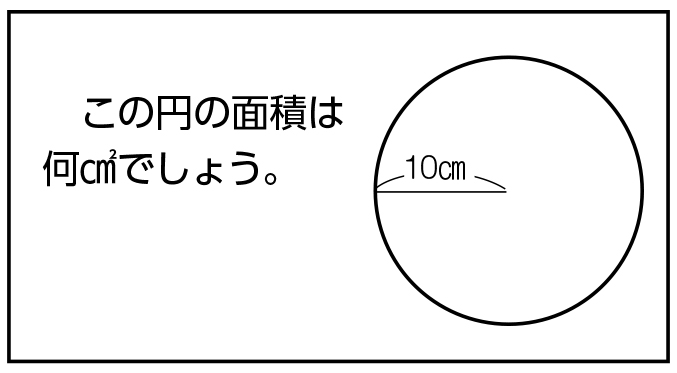
円 面積の計算 計算サイト



小6算数 円の面積 指導アイデア 1 みんなの教育技術
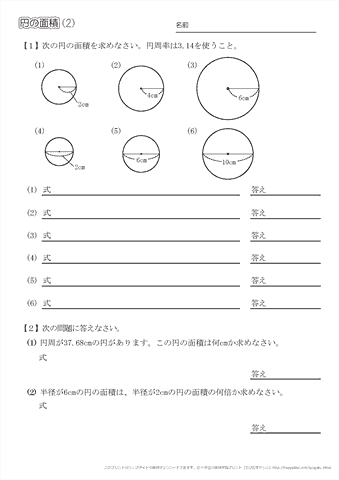



小学6年生の算数 円の面積 問題プリント ちびむすドリル 小学生



実践記録算数5年




無差別級算数 円の面積 2 解答 受験算数に挑戦



円積率 雑学のソムリエ




円の面積がpr 2になる納得の理由 図形を使った証明 数学の面白いこと 役に立つことをまとめたサイト




File 円の面積 Png Wikimedia Commons



1




円の面積の求め方を自主学習ノートで復習しましょう 円の面積の基本的な練習問題 円の面積の求め方を確認しておきます 円の面積 半径 半径 円周率 ちなみに 円周の長さの求め方は 学習ノート 数学ノート 学習
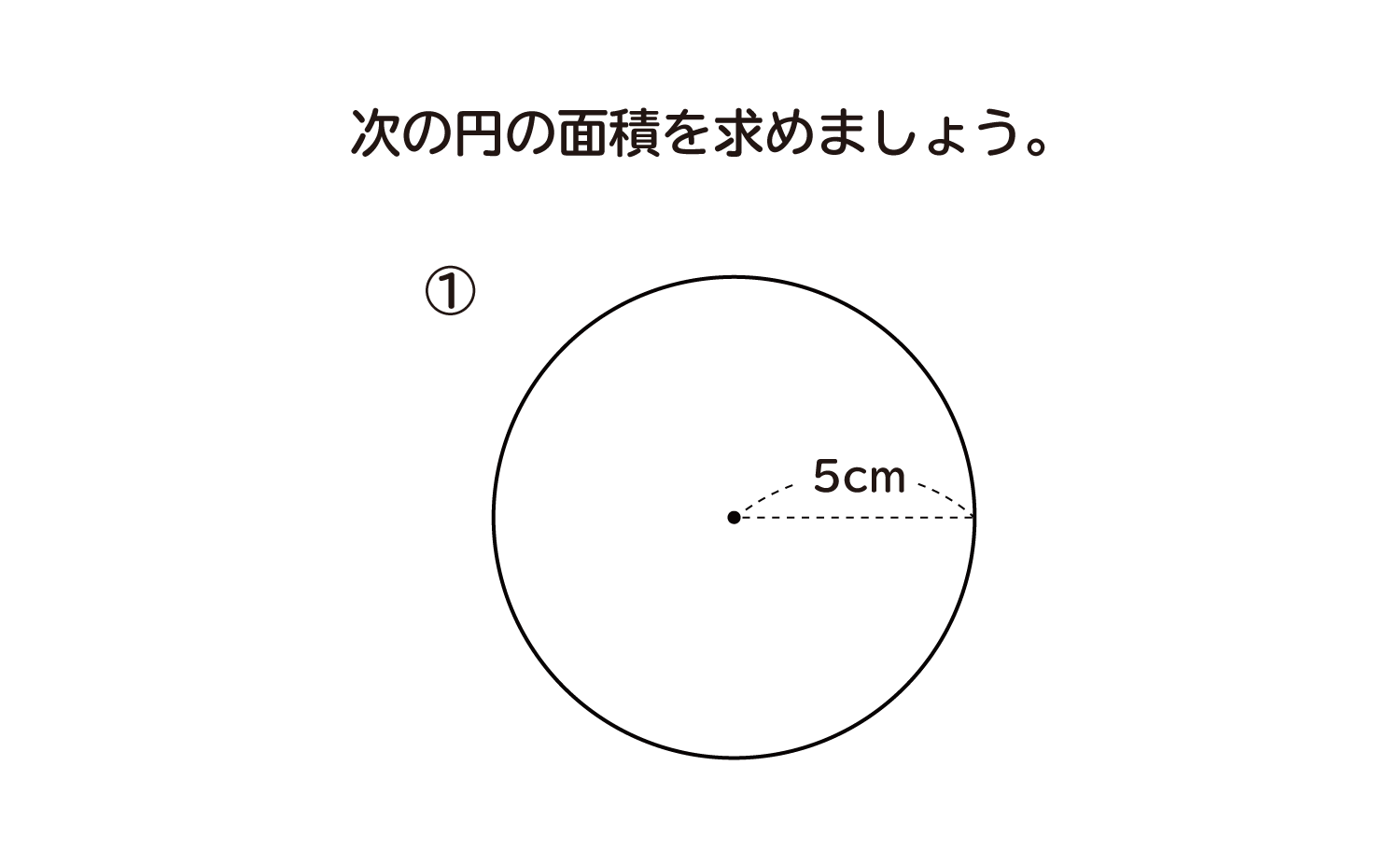



小学6年生 算数 無料問題集 円の面積 おかわりドリル




円の面積応用c 小学校 算数 学習 数学 勉強



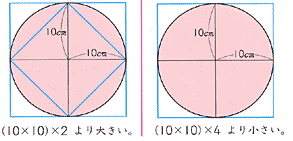
円の面積 算数の公式覚えてますか
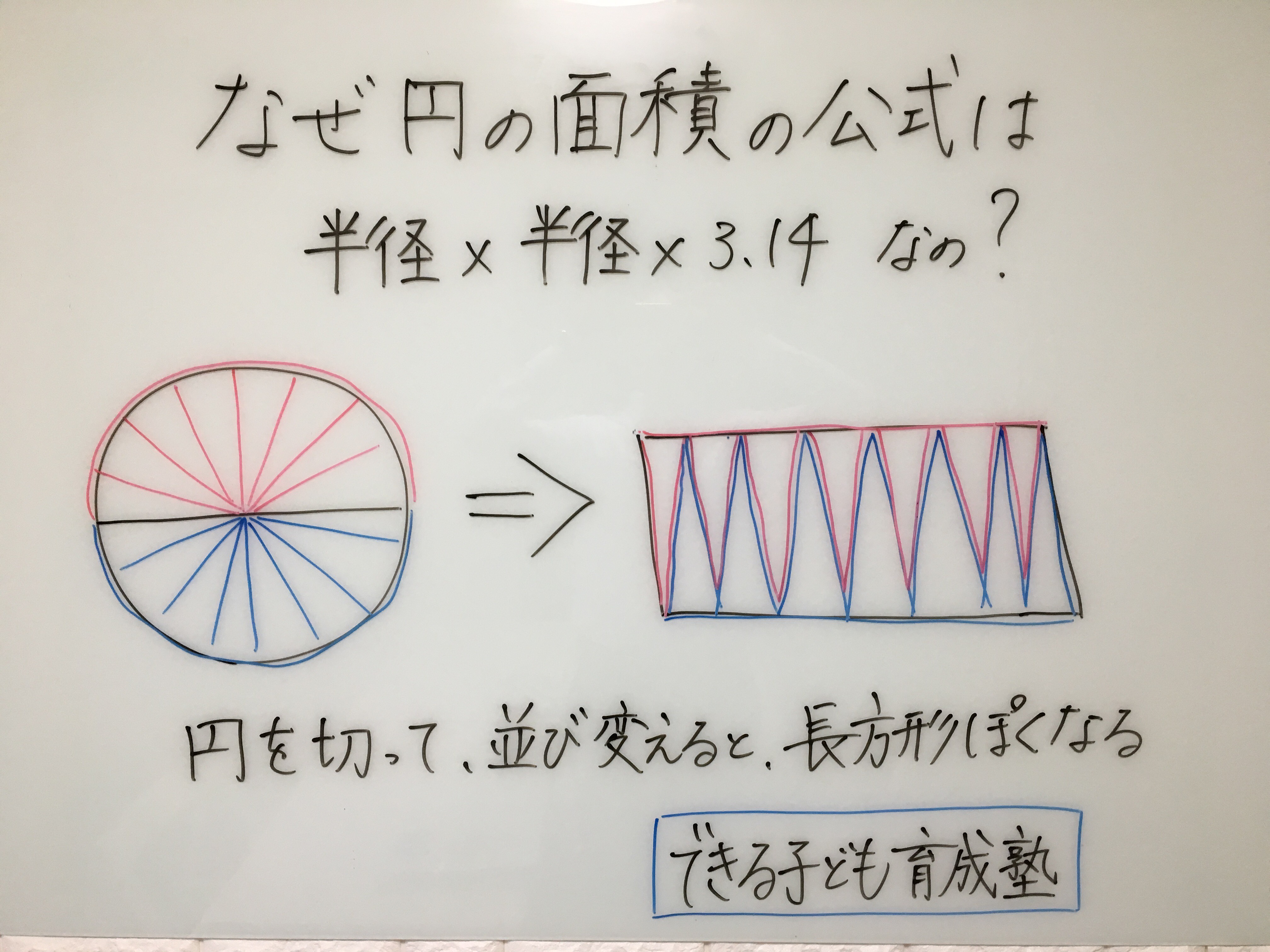



円の面積の求め方 公式 の理由を小学生に教える方法 元小学校教師が教える できる子ども育成塾 小岩 小学生専門の個別指導塾




円の面積はなぜ P R R なのか 公式の求め方を丁寧に解説 数学の面白いこと 役に立つことをまとめたサイト




すきるまドリル 小学6年生 算数 円の面積 無料学習プリント すきるまドリル 幼児 小学生の無料学習プリント



6年算数 円の面積 2 わかる教え方



6年算数 円の面積 2 わかる教え方
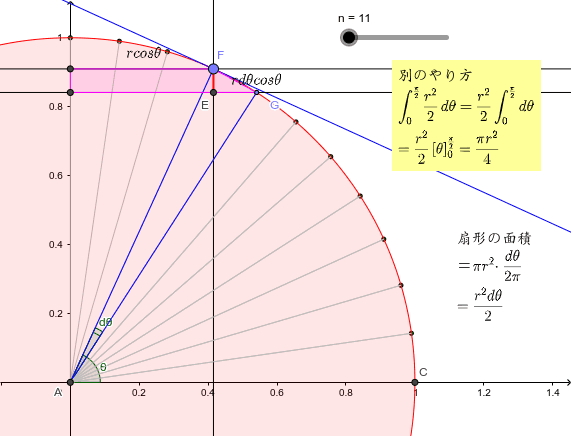



円の面積2 Geogebra



盲点の英単語 その8 円の面積の求め方を英語で言える 中学の英語をあなどってはいけない




円の面積 練習応用 Youtube



円周率 500 桁




円周と円の面積こんがらがらないように Explore Facebook
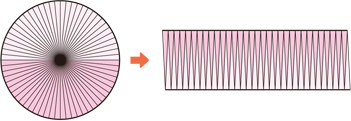



円の面積 算数用語集




円の面積の求め方 公式と計算例



6年算数 円の面積 2 わかる教え方




小6 算数 小6 2 円の面積 応用編 Youtube
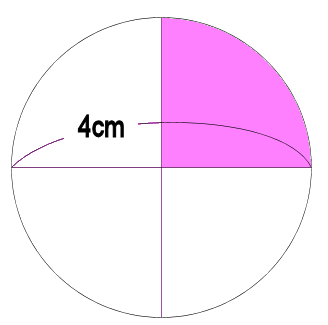



円の面積 正方形の中の円



6年算数 円の面積 2 わかる教え方
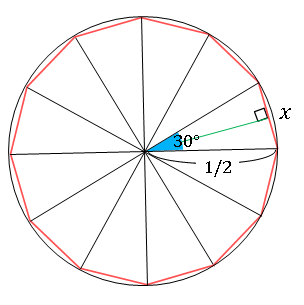



円の面積と周長 Excel Vba 数学教室




三角形の面積を外接円の半径を使って求める Schoolmath S Diary
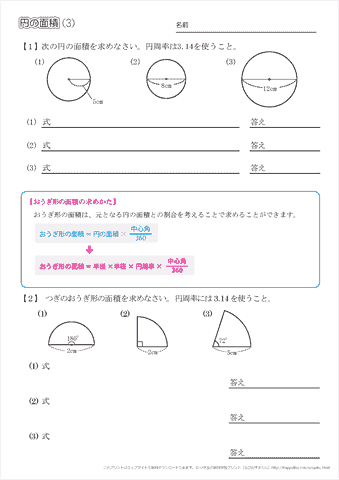



小学6年生の算数 円の面積 問題プリント ちびむすドリル 小学生




円の面積 円周の求め方 公式とやり方を解説 小学生向け 中学数学 理科の学習まとめサイト




円の面積の求め方と覚えるコツ なぜ半径 半径 3 14になるか アタリマエ



Asahi Com 朝日新聞社 円の面積 紙 球で実感 花まる先生公開授業 教育




円の面積 算数用語集
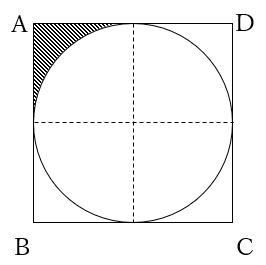



半径の分からない円の面積 中学受験プロ講師ブログ




円周率を使って 円の周囲の長さを計算する自主学習ノートを作りましょう 小数のかけ算を使います 5年生の後半から 6年生におすすめの自主学習です 円 半 円 おうぎ形の周囲の長さを計 学習 小学校 算数 学習ノート
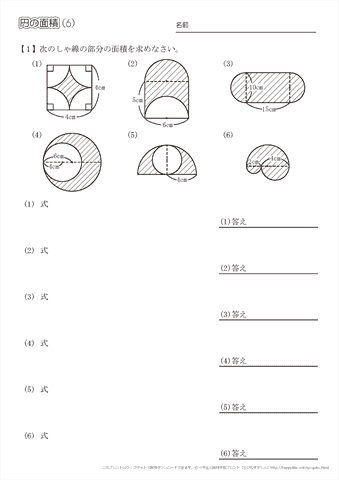



小学6年生の算数 円の面積 問題プリント ちびむすドリル 小学生
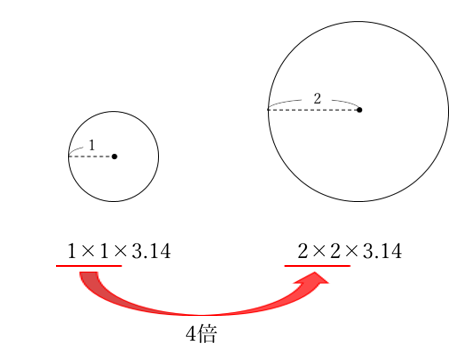



円の相似を利用した面積の計算 中学受験プロ講師ブログ
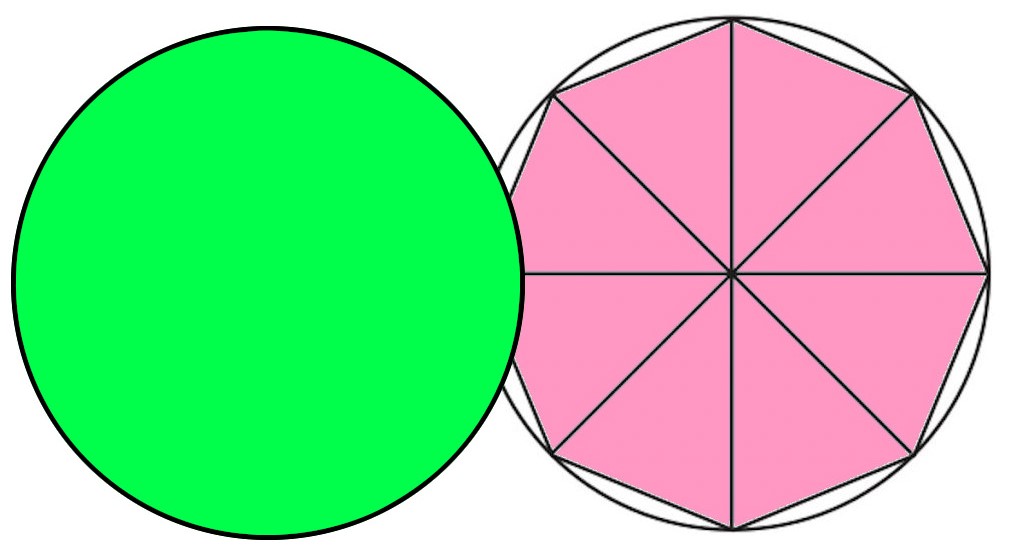



小6算数 円の面積 指導アイデア みんなの教育技術




円の面積 算数用語集
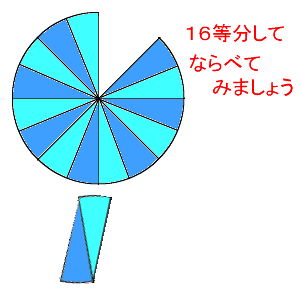



6年算数 円の面積 2 わかる教え方




円の面積の公式 円周の求め方と間違えないようにしよう 中学や高校の数学の計算問題



1
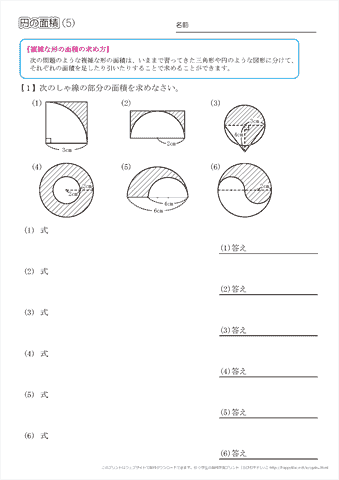



小学6年生の算数 円の面積 問題プリント ちびむすドリル 小学生
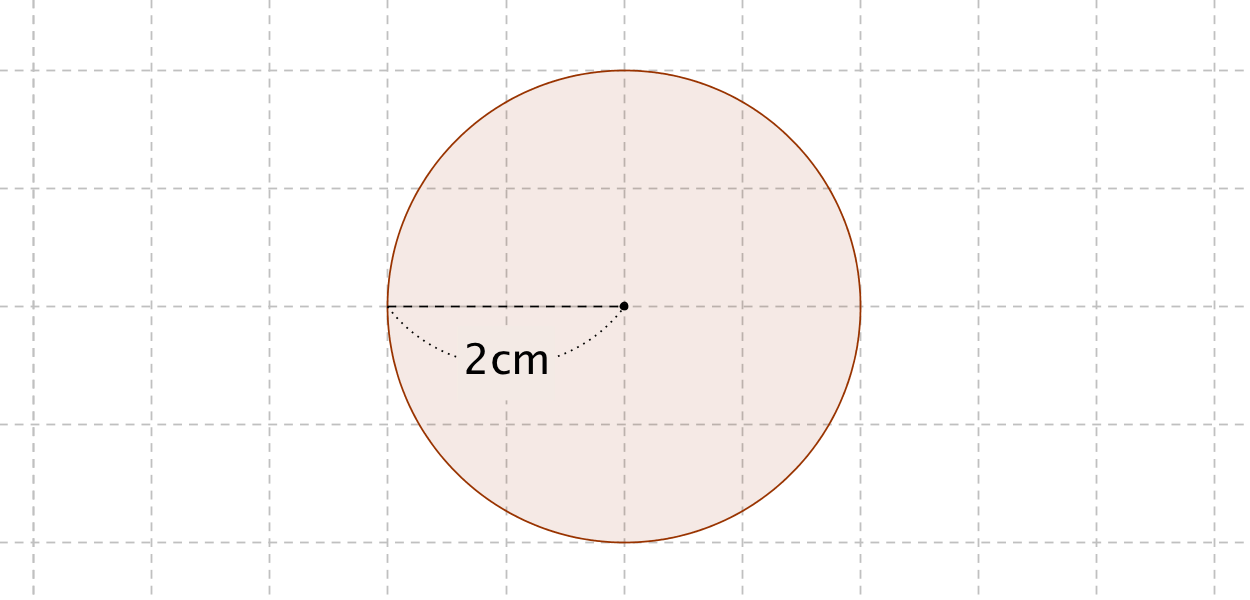



円の面積の公式 算数の公式




山と数学 そして英語 小学校算数 円の面積に関する応用問題
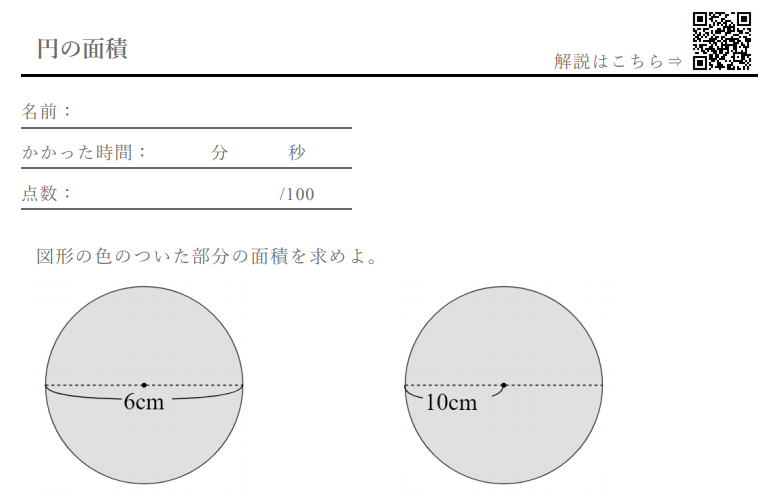



円 の面積 計算ドリル 問題集 数学fun




中学数学 円の面積の求め方 の公式を1発で覚えてしまう裏技 Qikeru 学びを楽しくわかりやすく
コメント
コメントを投稿